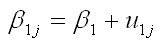
5.5.4. Model 4: model with varying intercepts and slopes

Where the random slopes coefficient is:

In this model an overall line relating the chance of someone voting with age is fitted, with intercept and slope . The change in the intercept for country j is and the change in the slope for country j is . If the overall relationship between the chance of voting and age is positive and is positive then the line is steeper than the overall gradient for country j. If the overall relationship between the chance of voting and age is positive and is negative then the line is less steep than the overall gradient for country j. For each country both the intercept and slope for the estimated relationship between the chance of voting and age can vary from the overall line. Hence the relationship between and is also of interest in Model 4, and this is summarised by the covariance term , . If the overall relationship between chance of voting and age is positive and is positive, this means that a line with a higher than overall intercept is also likely to have a steeper than overall slope. Hence the country-specific lines will diverge as shown in diagram (A) below. If is negative the country-specific lines will converge as shown in diagram (B) below. If there is no obvious pattern between intercept and slope, as shown in diagram (C), the estimated value of will be zero.