Extending the model (Model 3)(page 3/5)

Now we extend the model to include an explanatory variable -age, which has been centred around its mean. This is Model 3.

1. We now re-estimate the model (press 'more' on top left of programme window).

   

   We now see that age has a positive coefficient (0.014) which is statistically significant (i.e. more than twice its standard error which is shown in brackets after the estimate and in this case is 0.003). A rule of thumb is to compare twice the standard error with the absolute (ignore sign) value of the coefficient. To do this exactly we would use 1.96 standard errors but as 1.96 is close to two it is a useful approximation to simply double it. As we can see 0.14 > 0.006 so this coefficient is statistically significant. As people get older they are more likely to vote. There is still considerable variation between countries (0.307). Conditional on knowing the age of each person in the model, so age does not explain all the country level variation in voting. We could produce a caterpillar plot of the residuals as before but we will now produce another kind of plot - one showing the predicted values. Choose model > predictions



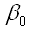2. Click on , and



3. Choose c20 as the output column and click 'calc'.
4. Now go to graphs, and choose customised graphs and set up the graph menu like this -a separate line for each country relating the predicted value of turnout on the log odds scale (c20) to (centred) age.
5. Click on apply.

   

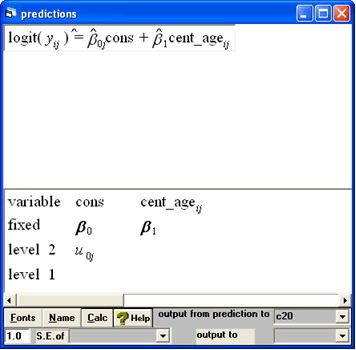
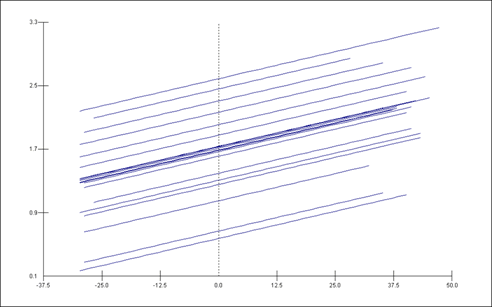
   We now see a graph with 20 parallel lines -the gradient is positive. As people get older they are more likely to vote. On the centred age scale, 0 represents the average value of age -around 47. We can see that there is variation in terms of where the lines cross the vertical line at x=0; a linear effect of age does not explain all the country level variations in voting.